МОДЕЛИРУЯ ТРАНЗИТЫ:
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ СОЦИО-ПОЛИТИЧЕСКИХ ФЕНОМЕНОВ
Кто мы
Подходы и инструментарий фрактальной геометрии успешно применяются во многих естественных науках и прикладных отраслях знания. Фрактальное моделирование – это относительно новый, перспективный способ создания компьютерных симуляций. Но это лишь один из способов моделирования, над которыми работает наш коллектив. В 2009 г. в Державинском университете группой исследователей-«модельеров» был создан Центр фрактального моделирования социальных и политических процессов – ЦФМ. В эту группу входят не только специалисты по фрактальной геометрии – мы изначально не замыкались лишь на фракталах. ЦФМ это один из немногих в стране центров, которые призваны продвигать методы “social simulation” в самом широком смысле. Хотя, конечно, именно фрактальное моделирование стало нашим брендом. На данный момент ЦФМ является лидером в разработке фрактальных моделей социо-политических феноменов (за исключением экономики).
У нас есть хороший опыт разнообразной работы: мы пишем компьютерные программы, осуществляем грантовые проекты, занимаемся издательской деятельностью. С самого начала ЦФМ активно сотрудничает с Центром исследования политических трансформаций и рядом других научных групп.
Наша инфраструктура и некоторые достижения
С 2005 г. исследовательский коллектив разрабатывает компьютерные модели для имитации исторических и политических феноменов. Наша методологическая инициатива была поддержана РФФИ. Д. Жуков и С. Лямин являлись/являются руководителями трёх проектов РФФИ, в рамках которых создавались теоретические основы и инструменты компьютерной симуляции нелинейных процессов:
— проект №14-06-00093-а «Приложение теории самоорганизованной критичности к изучению исторических процессов», 2014 – 2016 гг.;
— проект №10-06-00250-а «Компьютерное моделирование модернизационных процессов средствами фрактальной геометрии», 2010 – 2011 гг.;
— проект № 12-06-31111 мол_а «Исследование институциональной модернизации средствами компьютерного фрактального моделирования», 2012 – 2013 гг.
Наши проекты развивают междисциплинарную методологию, содействуют интеграции математических методов и синергетических представлений в социально-гуманитарную сферу.
Разработанная при поддержке РФФИ методология интегрировалась в несколько крупных исследовательских программ по политологии и истории. Для этих программ были созданы математические модели, описывающие модернизацию городской социальной среды в пореформенной России, динамику административно-политических институтов крупного государственного образования, демографическое поведение аграрного населения Центральной России второй половины XIX – XX вв., институциональную модернизацию в историческом прошлом и в современной России, динамику российского фронтира, взаимодействие аграрного социума и природной среды в Центральной России.
В ходе данных исследований продемонстрирована эвристическая продуктивность предложенных фрактальных моделей, обнаружены и разъяснены некоторые нелинейные эффекты, возникающие в социальных и политических системах, находящихся в состоянии качественной трансформации, в состоянии транзита. Разработанные инструменты (процедуры моделирования, математический аппарат и программное обеспечение моделей, технологий формализации исходных данных и пр.) используются для решения конкретных историко-политологических задач.
Довольно обширный список проектов, исполнителями которых являются наши сотрудники, обусловлен именно тем, что в этих проектах используются модели и инструменты, разработанные в ЦФМ.
Для реализации этих моделей и для проведения с их помощью компьютерных экспериментов созданы соответствующие компьютерные программы. Участники нашего коллектива получили два свидетельства Роспатента о регистрации программ («Фракталопостроитель Модернофрактал», № свидетельства 2011619003 от 18 ноября 2011 г.; «Фракталопостроитель Фрактлокластер», № свидетельства 2013612804 от 14 марта 2013 г.).
Благодаря поддержке РФФИ та версия фрактального моделирования, которую мы развиваем, получила признание научного сообщества. Это выразилась в публикации статей в иностранных и форвардных российских изданиях под эгидой Ассоциации «История и компьютер». Полученные результаты, являющиеся уникальными для социальных и политических дисциплин, опубликованы (в т.ч. – за рубежом) и представлены исследовательскому сообществу на авторитетных научных конференциях, в частности: X, XI, XII и XIII Международные конференции Ассоциации «История и компьютер», VI Всероссийский Конгресс политологов, XXXII Аграрный симпозиум и др.
В 2007 – 2010 гг. опубликованы три монографии, в которых обозначены методологические подходы к использованию фрактальной методологии в социальных науках (Жуков Д.С., Лямин С.К. «Живые модели ушедшего мира: фрактальная геометрия истории»; Жуков Д.С., Лямин С.К. «Метафоры фракталов в общественно-политическом знании»; Жуков Д.С., Канищев В.В., Лямин С.К. «Фрактальное моделирование историко-демографических процессов»). Результаты в области фрактального моделирования опубликованы за рубежом в журнале, входящем в Web of Science и SCOPUS (Zhukov, D. & Lyamin, S.Computer Modeling of Historical Processes by Means of Fractal Geometry // Historical Social Research. No. 133. HSR Vol. 35 (2010) 3. P. 323-350; Dmitry Zhukov, Valery Kanishchev, Sergey Lyamin. Fractal Modeling of Historical Demographic Processes // Historical Social Research. 2013. No 2.).
Наш коллектив выпускает журнал «Fractal simulation» (ISSN 2222-0674). Журнал издаётся на некоммерческой основе, не взимает плату с авторов за публикации и с читателей за доступ к статьям. Двухлетний импакт-фактор РИНЦ 2012 без самоцитирования 2,667. Журнал учреждён в 2011 г. Тамбовским государственным университетом (Центром фрактального моделирования). По соглашению с университетом издателем журнала является общественная организация «Инетернум». Журнал размещается в elibrary.ru в полнотекстовом виде в открытом доступе. Сайт журнала http://www.ineternum.ru/ineternum/aaa_fractal_centre/zhur/zhur.html Для вывода данного издания на международный уровень в 2013 г. была учреждена англоязычная версия «Fractal simulation» (ISSN 2307-9711).
Журнал является специализированным и посвящен применению фрактального моделирования и иных средств компьютерного моделирования для исследования различных (в том числе социально-политических) феноменов. Фрактальное моделирование социально-политических систем – это сфера, в которой отечественные исследователи имеют на данный момент приоритет, и издание журнала поможет этот приоритет закрепить.
Электронные копии упомянутых монографий и ряда статей, а также доклады, посвящённые фрактальному моделированию в социально-гуманитарных науках, прочие результаты деятельности ЦФМ представлены на сайте Центра – http://www.ineternum.ru/ineternum/aaa_fractal_centre/index.html.
Наша методологическая инициатива
Средства и подходы фрактальной геометрии (как направления в теории хаоса) предоставляют исследователю удобный инструментарий для изучения процессов, включающих фазовые переходы, «парадоксальную» несоразмерность причин и следствий, иные нелинейные эффекты. Фрактальные модели обладают существенными эвристическими возможностями именно для имитации нелинейности.
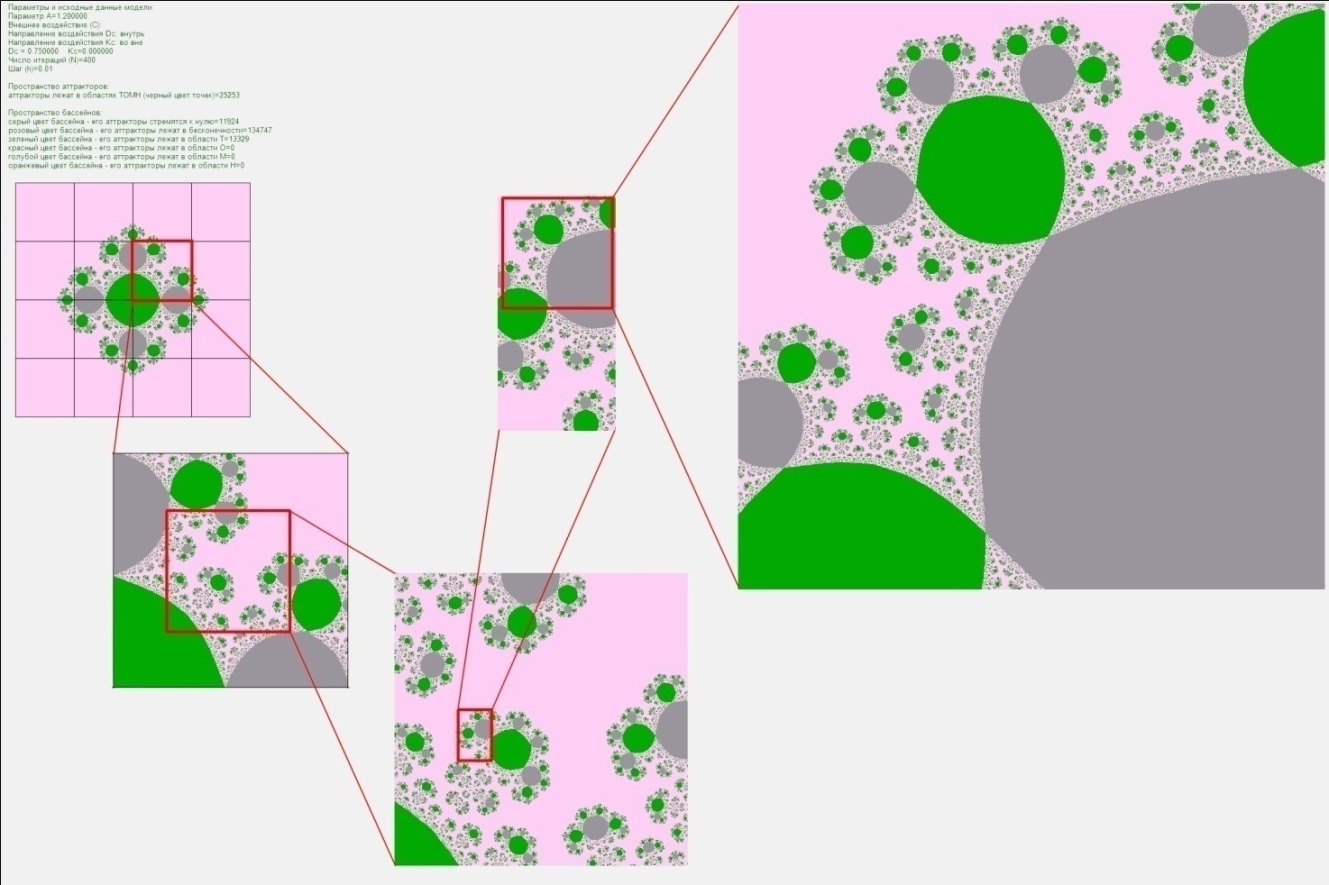
В результате предшествующих исследований нам удалось разработать и представить общую фрактальную модель перехода (ОФМП) в качестве математико-логической матрицы, описывающей некоторые механизмы и эффекты трансформации (и, в частности, транзита) социальных систем. ОФМП позволяет исследователь аттракторы и бассейны начальных состояний систем. ОФМП реализуется с помощью специальной программы-фракталопостроителя Модернофрактал, которую мы разработали.
Математический аппарат наших моделей, основанных на построении алгебраических фракталов (в частности, ОФМП), содержит процедуры, описанные Бенуа Мандельбротом для получения алгебраических фракталов. В классические алгоритмы вносятся изменения, добавляются новые математические условия с целью привести в соответствие математический аппарат фракталопостроителей со свойствами моделируемых объектов.
Хорошо калиброванная и верифицированная модель позволяет проводить компьютерные эксперименты с виртуальными отображениями реальных объектов и процессов. Поскольку, как правило, мы не имеем возможности произвольно экспериментировать с социальными и политическими явлениями, то их модели можно использовать как своего рода «эвристическую машину» для производства гипотез, выявления потенциалов и для прогнозирования.
Разработанные модели основываются на достижениях теории хаоса (в частности – синергетики и фрактальной геометрии), позволяют обнаруживать и имитировать нелинейные эффекты, возникающие в динамических системах в результате взаимодействия ряда управляющих факторов. Нарушение соразмерности причин и следствий, «спонтанная» активность или, напротив, «чрезмерная» инертность изучаемой системы, способность к взрывообразному разрушению или к самоструктурированию во время фазового перехода – все эти эффекты крайне трудно поддаются обобщению в рамках традиционных линейных моделей. Между тем, с описанными явлениями исследователи довольно часто сталкиваются при изучении социальной и политической реальности. В рамках общественно-политических наук также продемонстрировал свою эффективность и понятийный аппарат теории хаоса: для анализа ситуаций активно используются такие конструкты как «бассейн исходных состояний», «аттрактор», «точка бифуркации». Эти объекты возникают в ходе компьютерных экспериментов с фрактальными моделями.
Значительные усилия коллектива были направлены на исследования возможности использования ОФМП для описания процессов и эффектов транзита и форсированной институциональной модернизации – применительно к системам, находящимся вблизи фазового перехода («взрывообразной» социальной трансформации).
Компьютерная среда ОФМП является хорошим «производителем» гипотез и виртуальных сценариев. Генерируя эффекты теории хаоса, эта модель предлагает исследователю инструментарий для того, чтобы выйти за рамки устоявшихся интерпретаций. Внешне парадоксальные события, возникающие в модельных сценариях, в действительности соответствуют общим положениям теории хаоса и потому являются эвристически ценными объяснительными схемами для эмпирических фактов.
Общая фрактальная модель перехода позиционируется как модельная основа для разработки социальных технологий, альтернативных катастрофическим сценариям и, в частности, «опрокидыванию».
Некоторые политологические интерпретации наших экспериментов
Посредством Модернофрактала были поставлены несколько серий экспериментов. Мы выстроили виртуальные сценарии институциональной модернизации, исходя из экспертных оценок по поводу величин управляющих факторов.
Модернизация – так, как она предстаёт в ОФМП – является неклассической, турбулентной. Она содержит качественные скачки, парадоксальные, на первый взгляд, нелинейные эффекты. Подобная модель модернизации, как видится, более применима к российским реалиям. И более того – эта модель соответствует синергетическим представлениям, положениям теории хаоса, что позволяет преодолеть исходное линеарное представление о модернизации, сформировавшееся под воздействием внеисторических эталонных концепций.
В рамках классической линеарной модели модернизации институциональная трансформация должна была осуществляться лишь в формате «медленной эволюции», а революционные скачки третировались как «патологические». Однако эта схема признаётся исследователями устаревшей – и разнообразные неклассические представления о модернизации развиваются как попытка адаптировать теорию модернизации к теории хаоса.
Было признано, что модернизационные скачки возможны, естественны и, более того, необходимы. Современные представления об институциональной модернизации предусматривают возможность как закономерных нормальных, так и «искусственных» спровоцированных из-вне скоротечных институциональных трансформаций.
Совокупность нелинейных эффектов модернизации мы обозначили термином «турбулентная» модернизация. В рамках представлений о «турбулентной» нелинейной модернизации прослеживается попытка отказаться от логики больших причин и больших следствий, изменить отношение к малым воздействиям. Средства и подходы теории хаоса (в т.ч. синергетики, фрактальной геометрии) предоставляют исследователю, как уже отмечалось, удобный инструментарий для изучения процессов, включающих фазовые переходы, «парадоксальную» несоразмерность причин и следствий, иные нелинейные эффекты. Микроскопические явления не только обеспечивают специфичность модернизации, но иногда прямо определяют её макро-успех или не успех. Несильные, «низкоэнергетические» воздействия на систему могут вызвать в ней катастрофические самоусиливающиеся процессы.
Для «турбулентной» модернизации характерны фазовые переходы: скачки, «прорывы», когда перестаёт действовать логика «больших причин и больших следствий». Как обратная стороны медали: система может проявлять «неестественную» пассивность, эффективно гася модернизационные импульсы и не реагируя на внешние вызовы. Эффекты турбулентной модернизации могут быть весьма неожиданными для стороннего наблюдателя. Представим, что мы решили приготовить чай и поставили чайник на плиту, но по мере подогрева в кипящей воде начинают образовываться кристаллики льда. Однако, это – своего рода «непарадоксальные парадоксы», которые лишь указывают на существо явления.
«Турбулентная» модернизация не является равномерной – она охватывает в разной мере разные институты, слои и пространства, что может приводить к «противотечениям» (к формированию замкнутых архаизированных сегментов) и даже к структурным противоречиям. Так возникает институциональная структура, которую американский историк Альфред Рибер назвал «осадочным обществом». Здесь модернизированные институты не замещают (или не полностью замещают) традиционные, а надстраиваются над ними. Как результат: наличие социальной инерции, потребность в модернизационных сверх-усилиях, институциональные конфликты.
Форсированная институциональная модернизация – а именно форсированный способ развития, по общему мнению исследователей, характерен для современной России – во многих случаях просто обречена на прохождение зон турбулентности.
Как «выглядят» наши эксперименты и наши программы
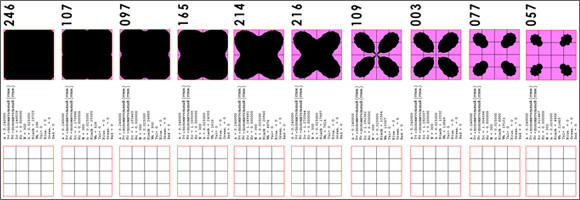
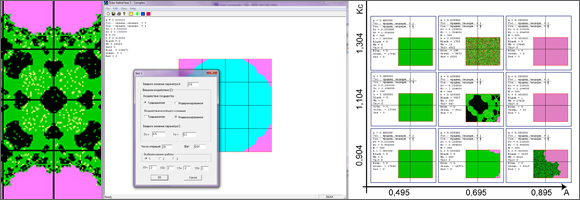
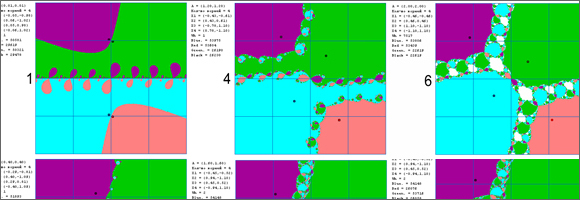
Вот некоторые наши программы и примеры изображений, которые генерируются фракталопостроителями. Такие изображения (аттракторы, бассейны исходных состояний, траектории в фазовом пространстве) можно подвергнуть качественной интерпретации.
Развитие моделирования сдерживается недостатком программного обеспечения, доступного специалистам-гуманитариям. ЦФМ имеет довольно обширный опыт создания программ, ориентированных именно на исследовательские нужды в социо-гуманитарных областях знания. Фракталопостроитель Модернофрактал V 5.1 – наиболее масштабная, но не единственная, разработка на данный момент. Созданы также программы «Фракталокластер», «Менталофрактал», «Демофрактал», «Империя» и др.
Модернофрактал V 5.1
Программа Модернофрактал V 5.1 предназначена для проведения компьютерных экспериментов с ОФМП и осуществляет процедуры построение алгебраического фрактала. Математический аппарат программы содержит итерируемую формулу, а также ряд математических условий, которые позволяют отождествить геометрический смысл операций над комплексными числами с результатами взаимодействия факторов модели. Итерируемая формула генерирует череду чисел, которая задаёт траекторию изображающей точки в двухмерном фазовом пространстве. Программа генерируют изображения бассейнов системы и её аттракторов в фазовом пространстве. Бассейны – совокупности начальных состояний, стартуя из которых точка попадёт в один и тот же аттрактор. Аттракторы фиксируются как точки, в которые попадёт система после множества итераций (подстановок значений в итерируемую формулу), если, конечно, эти точки стабильны и воспроизводятся вновь и вновь с высокой степенью приближения в серии последних итераций. Разработчики: Дмитрий Жуков, Сергей Лямин, Юлия Мовчко. Подробное описание программы можно найти в её справочной системе на сайте ЦФМ по этой ссылке.
Демофрактал
Эта программа, также как и Модернофрактал, представляет собой генератор алгебраических фракталов посредством итерирования формулы, которая представляет собой своего рода исходный код для развития исследуемой системы. Но, в отличие от Модернофрактала, Демофрактал был создан для решения узких задач – для моделирования демографических процессов.
Менталофрактал
Самая первая версия построителя алгебраических фракталов, созданная в ЦФМ для проектов по изучению модернизации социальных сред и институтов. Программное обеспечение Менталофрактала позволяет проводить своего рода виртуальные социальные эксперименты. Для этого мы можем изменить значения тех или иных факторов и проследить, как изменятся потенциалы и аттракторы социума в данном экспериментальном случае. Это существенно расширяет наши эвристические возможности, поскольку в реальном мире такие эксперименты, естественно, невозможны.
Фракталокластер
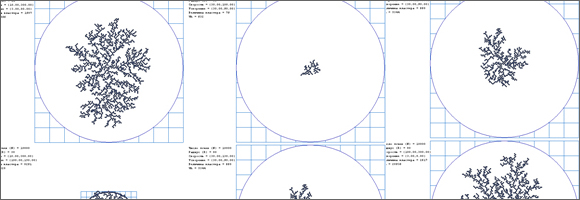
Эта программа представляет собой виртуальную среду, в которой под воздействием ряда факторов растёт фрактальный кластер. Кластер является результатом «бомбардировки» точками некоторого основания. Причём, значимые факторы среды варьируются случайным образом, но в установленном диапазоне. Значимые параметры процесса кластерообразования могут быть определены пользователями в соответствии с основными факторами, воздействующими на моделируемый объект. Построение стохастических фракталов, позволяет имитировать реальные процессы. Подобные фракталы будут отображать результаты процессов, которые сочетают в себе элементы закономерности и случайности. К числу таких процессов относятся практически все социальные процессы, описываемые статистическими законами. Подобного рода построители стохастических фрактальных кластеров широко используются для изучения разного рода феноменов: развитие сетей, динамика фронтов вытеснения и пр.
Империя
Программа Империя создавалась для решения частной задачи — исследования эволюции крупных гетерогенных государственных образований, а именно для построения сценариев распределения полномочий между властными органами центра и периферии. Программа осуществляет решение уравнения n-ной степени методом Ньютона, фиксируя аттракторы (собственно, искомые решения) и бассейны начальных состояний (отправных значений). Исследователи заинтересованы, главным образом, в изучении бассейнов, поскольку они демонстрируют потенциалы и возможности развития исходной ситуации. Подобный подход оказался довольно продуктивным, поскольку, как можно было убедиться на фактологическом материале, итог имперского развития обнаруживает сильную зависимость от начальных условий.